In the last instalment we examined how stellar masses were obtained from binary stars, for example, from their radial velocity curves. In this instalment we go further to show how other stellar properties including luminosity and radius can be obtained, as well as effective (or surface) temperature.
We will start with The Mass-Luminosity relation, which enables us to infer the actual brightness of a main sequence star based on its mass, is actually due to data from visual and other binaries. Recall the sample problem we looked at in Part (7):
The semi-major axis of the true relative orbit for Sirius A and B is 7½" and the distance from the Sun to Sirius is 2.67 pc. If the period of the Sirius binary system is 50 years and the component B is found to be twice as far from the center of mass as component A, then find the total mass of the Sirius system and the masses of each component.
We first obtained the mass total:
m(A) + m(B) = (d a")^3/ P^2 = (2.67 pc x 7.5")/(50 yr)^2 = 3.2 solar masses
So:
m(A) + m(B) = 3.2 M_s
In terms of the center of mass, we then used the sketch:
A O------------x cm-------------------------o B
where: xB = 2 (xA)
Then: xB/xA = 2, and:
m(A)/m(B) = xB/xA = 2/1
so: m(B) = ½ m(A)
(since the more massive star is always closer to the center of mass)
Thus, m(A) ~ 2.13 M_s, and m(B) ~ 1.06 M_s
Now the next question is: Can we obtain the actual brightness of either of these? The answer is we can, but only for star (A) or Sirius A. This is because the Mass-Luminosity relation only applies to stars on the Main Sequence, hence gives the mass in terms of the solar mass (the Sun being used as a 'standard' for the stars on the Main Sequence).
From the Mass-Luminosity relation we have:
L’/L = (M’/M)^3.5
Or Log (L’/L) = 3.5 Log (M’/M)
where L, M refer to solar values and L', M' to stellar values. In this case, for Sirius A, M' = 2.13 solar masses, so (M’/M) = 2.13, and:
3.5 (Log 2.13) = Log (L'/L) = 3.5 (0.3283) = 1.149
But: antilog (1.149) = 14.09
Or: L' = 14 L approx.
So, Sirius A is about 14 times more luminous than the Sun.
Another example:
The intrinsic brightness (luminosity) of Regulus is greater than the Sun's by a factor 120x. Find the approximate mass of Regulus.
Here: L'/L = 120 so Log (120) = 3.5 Log (M'/ M)
and we are seeking to find M' in terms of M.
Log (120) = 2.079 = 3.5 Log (M'/ M)
Or:
0.594 = Log (M'/M)
Taking antilogs of each side:
3.93 = (M'/M) or M' = 3.93 M
So Regulus is approximately 4 times the mass of the Sun.
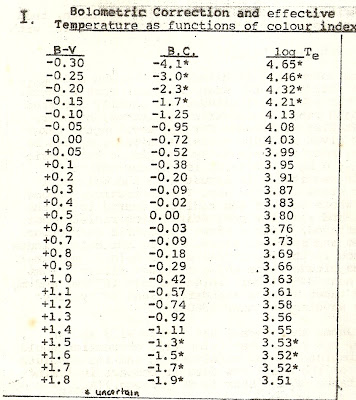
In the sections on 'Tackling Simple Astronomy Problems', we referred to "absolute magnitudes". However, in stellar properties' analysis we need to refine this to deal with "absolute bolometric magnitudes" because the brighter stars (or spectral class O and A mainly) require special "color" corrections usually referred to as "bolometric corrections". This refined system of "bolometric magnitudes" is thereby adjusted so the bolometric corrections are small for stars like the Sun (e.g. G class or later) but large for very hot stars where most of the radiated energy is in the unobservable ultraviolet (UV). The Table shown gives bolometric corrections for different temperatures and spectral types.
Note the difference (B - V) is the "color index" representing the difference in magnitudes m_B and m_V, e.g. (m_B - m_B) where m_B is the apparent magnitude from a bule filter and m_V is the apparent magnitude from the standard yellow or visual filter - most senstive to wavelengths near 550 nm.
Now, if the absolute bolometric magnitude (M_bol) of a star is known, then its luminosity can be found as a function of the Sun's luminosity with the relation:
Log (L'/L) = 0.4 (M_bol - M_bol*)
where M_bol is for the Sun and M_bol* is for the star. Note that any given absolute visual magnitude (M_V) can be changed to an absolute bolometric magnitude by applying a bolometric correction such that:
M_bol* = M_V* + B.C.
Example Problem:
The star Almach (Gamma Andromeda) has (B - V) = +1.3 and an apparent visual magnitude m_V* = 2.16. What bolometric correction should be applied? Also, find the absolute visual magnitude M_V* and the absolute bolometric magnitude M_bol* of the star. How does it compare in luminosity to the Sun? (The distance of Almach is 80 pc)
Solution:
From the Table:
We find (B - V) = +1.3 corresponds to B.C. = - 0.92.
The absolute visual magnitude can be found from the apparent visual magnitude by using the distance modulus, cf. Tackling Simple Astronomy Problems 4, e.g.
http://brane-space.blogspot.com/2011/07/tackling-simple-astronomy-problems-4.html
Thus:
(m - M) = (m_V* - M_V*) = 5 log (D) - 5
and:
M_V *= m_V* - 5 log (D) + 5 = 2.16 - 5 log (8o) + 5
M_V* = 2.16 - 5(1.903) + 5 = -2.36
The absolute bolometric magnitude is:
M_bol* = M_V* + B.C. = (-2.36) + (-0.92) = -3.28
The relative luminosity as a function of absolute bolometric magnitude is:
Log (L'/L) = 0.4 (M_bol - M_bol*) = 0.4 (4.63 - (-3.28))
Log (L'/L) = 0.4(7.91) = 3.16
antilog 3.16 =1445 so: L' = 1445 L
Other Problems:
(1)The apparent V-band (filter) magnitude of a star is 8.72, and it requires a bolometric correction of -0.48. Find the apparent bolometric magnitude of the star. (Hint: Apparent bolometric magnitudes are obtained in an analogous way to the absolute forms)
(2) A star has a color index (B - V) of +1.0 and its apparent B-band magnitude is 6.4. The corresponding bolometric correction is - 0.5. Find the apparent bolometric magnitude of the star.
(3) The star Alhena in the constellation Gemini is at a distance of 30 pc. If it has (B - V) = 0.00, and m_V = +1.93, find the apparent B-band magnitude, m_B.
Also find the absolute visual magnitude and the absolute bolometric magnitude of the star.
Find the luminosity of Alhena in terms of the solar value.
We will start with The Mass-Luminosity relation, which enables us to infer the actual brightness of a main sequence star based on its mass, is actually due to data from visual and other binaries. Recall the sample problem we looked at in Part (7):
The semi-major axis of the true relative orbit for Sirius A and B is 7½" and the distance from the Sun to Sirius is 2.67 pc. If the period of the Sirius binary system is 50 years and the component B is found to be twice as far from the center of mass as component A, then find the total mass of the Sirius system and the masses of each component.
We first obtained the mass total:
m(A) + m(B) = (d a")^3/ P^2 = (2.67 pc x 7.5")/(50 yr)^2 = 3.2 solar masses
So:
m(A) + m(B) = 3.2 M_s
In terms of the center of mass, we then used the sketch:
A O------------x cm-------------------------o B
where: xB = 2 (xA)
Then: xB/xA = 2, and:
m(A)/m(B) = xB/xA = 2/1
so: m(B) = ½ m(A)
(since the more massive star is always closer to the center of mass)
Thus, m(A) ~ 2.13 M_s, and m(B) ~ 1.06 M_s
Now the next question is: Can we obtain the actual brightness of either of these? The answer is we can, but only for star (A) or Sirius A. This is because the Mass-Luminosity relation only applies to stars on the Main Sequence, hence gives the mass in terms of the solar mass (the Sun being used as a 'standard' for the stars on the Main Sequence).
From the Mass-Luminosity relation we have:
L’/L = (M’/M)^3.5
Or Log (L’/L) = 3.5 Log (M’/M)
where L, M refer to solar values and L', M' to stellar values. In this case, for Sirius A, M' = 2.13 solar masses, so (M’/M) = 2.13, and:
3.5 (Log 2.13) = Log (L'/L) = 3.5 (0.3283) = 1.149
But: antilog (1.149) = 14.09
Or: L' = 14 L approx.
So, Sirius A is about 14 times more luminous than the Sun.
Another example:
The intrinsic brightness (luminosity) of Regulus is greater than the Sun's by a factor 120x. Find the approximate mass of Regulus.
Here: L'/L = 120 so Log (120) = 3.5 Log (M'/ M)
and we are seeking to find M' in terms of M.
Log (120) = 2.079 = 3.5 Log (M'/ M)
Or:
0.594 = Log (M'/M)
Taking antilogs of each side:
3.93 = (M'/M) or M' = 3.93 M
So Regulus is approximately 4 times the mass of the Sun.
In the sections on 'Tackling Simple Astronomy Problems', we referred to "absolute magnitudes". However, in stellar properties' analysis we need to refine this to deal with "absolute bolometric magnitudes" because the brighter stars (or spectral class O and A mainly) require special "color" corrections usually referred to as "bolometric corrections". This refined system of "bolometric magnitudes" is thereby adjusted so the bolometric corrections are small for stars like the Sun (e.g. G class or later) but large for very hot stars where most of the radiated energy is in the unobservable ultraviolet (UV). The Table shown gives bolometric corrections for different temperatures and spectral types.
Note the difference (B - V) is the "color index" representing the difference in magnitudes m_B and m_V, e.g. (m_B - m_B) where m_B is the apparent magnitude from a bule filter and m_V is the apparent magnitude from the standard yellow or visual filter - most senstive to wavelengths near 550 nm.
Now, if the absolute bolometric magnitude (M_bol) of a star is known, then its luminosity can be found as a function of the Sun's luminosity with the relation:
Log (L'/L) = 0.4 (M_bol - M_bol*)
where M_bol is for the Sun and M_bol* is for the star. Note that any given absolute visual magnitude (M_V) can be changed to an absolute bolometric magnitude by applying a bolometric correction such that:
M_bol* = M_V* + B.C.
Example Problem:
The star Almach (Gamma Andromeda) has (B - V) = +1.3 and an apparent visual magnitude m_V* = 2.16. What bolometric correction should be applied? Also, find the absolute visual magnitude M_V* and the absolute bolometric magnitude M_bol* of the star. How does it compare in luminosity to the Sun? (The distance of Almach is 80 pc)
Solution:
From the Table:
We find (B - V) = +1.3 corresponds to B.C. = - 0.92.
The absolute visual magnitude can be found from the apparent visual magnitude by using the distance modulus, cf. Tackling Simple Astronomy Problems 4, e.g.
http://brane-space.blogspot.com/2011/07/tackling-simple-astronomy-problems-4.html
Thus:
(m - M) = (m_V* - M_V*) = 5 log (D) - 5
and:
M_V *= m_V* - 5 log (D) + 5 = 2.16 - 5 log (8o) + 5
M_V* = 2.16 - 5(1.903) + 5 = -2.36
The absolute bolometric magnitude is:
M_bol* = M_V* + B.C. = (-2.36) + (-0.92) = -3.28
The relative luminosity as a function of absolute bolometric magnitude is:
Log (L'/L) = 0.4 (M_bol - M_bol*) = 0.4 (4.63 - (-3.28))
Log (L'/L) = 0.4(7.91) = 3.16
antilog 3.16 =1445 so: L' = 1445 L
Other Problems:
(1)The apparent V-band (filter) magnitude of a star is 8.72, and it requires a bolometric correction of -0.48. Find the apparent bolometric magnitude of the star. (Hint: Apparent bolometric magnitudes are obtained in an analogous way to the absolute forms)
(2) A star has a color index (B - V) of +1.0 and its apparent B-band magnitude is 6.4. The corresponding bolometric correction is - 0.5. Find the apparent bolometric magnitude of the star.
(3) The star Alhena in the constellation Gemini is at a distance of 30 pc. If it has (B - V) = 0.00, and m_V = +1.93, find the apparent B-band magnitude, m_B.
Also find the absolute visual magnitude and the absolute bolometric magnitude of the star.
Find the luminosity of Alhena in terms of the solar value.
No comments:
Post a Comment